Warum es wichtig ist, zentriert zu bleiben: Lehren aus gotischen Kathedralen zur Stabilität moderner Kranausleger

ABBILDUNG 2: Spitzen der Kathedrale von Reims, fertiggestellt um 1275.

Die Erbauer mittelalterlicher Kathedralen nutzten die Bauwerke als maßstabsgetreue Modelle in einem organischen Prozess. Die Reaktion der Struktur auf die einwirkenden Lasten signalisierte den Erbauern, dass Anpassungen am Entwurf erforderlich waren. „Was zum Teufel hat das mit dem Betrieb von Kränen zu tun?“, fragen Sie sich wahrscheinlich. Haben Sie Geduld.

ABBILDUNG 1: Schublinien in einer gotischen Kathedrale.

Das markanteste Merkmal gotischer Kathedralen ist wohl der Spitzbogen (Abbildung 1). Diese Bögen wirken der Schwerkraft mit horizontalen Kräften, sogenannten Schubkräften, entgegen. Die Funktion der Struktur besteht darin (ähnlich wie bei einem Kranausleger), diese Lasten sicher in den Boden zu befördern. Die Kombination dieser Schubkräfte mit dem Gewicht der Steinblöcke führt zu einer Schublinie, während die Last ihrem Weg zum Boden folgt.

Schublinien

Die Baumeister bemerkten, dass sich mit zunehmender Größe der Bauwerke Risse in den die Bögen tragenden Mauern bildeten. Der Verlauf dieser Schublinien bestimmte die Gestaltung der Kathedralen. Idealerweise sollten die Linien gerade nach unten zeigen. Die horizontalen Schublinien verhinderten dies jedoch. Um diesen Schublinien standzuhalten, wurden große Steinmauern, sogenannte Strebepfeiler, errichtet. Und als die Gebäude größer wurden, wurden horizontale Strebepfeiler hinzugefügt, um die oberen Mauern zu stützen.

Sie entdeckten, dass diese Risse entstehen würden, wenn die Schublinien weit über das Zentrum der Steinmasse hinausgehen. Ihre Lösung bestand darin, die Schublinien durch das Anbringen von Gewichten, sogenannten Spitzen, an den Strebepfeilern in die Vertikale zu drehen. Aus diesem Grund wurden diese wundervollen Statuen auf den Spitzen der Bauwerke angebracht (Abbildung 2).

Mitte des 19. Jahrhunderts begannen Ingenieure, das Verhalten von Mauerwerksstrukturen zu quantifizieren.1 Zu Beginn des 20. Jahrhunderts war das Konzept des „mittleren Drittels“ bei der Konstruktion von Mauerwerksstrukturen weit verbreitet.

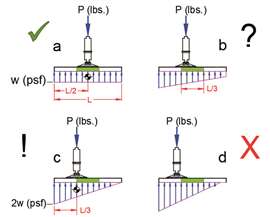ABBILDUNG 3: Ausleger, der von einer Kranmatte auf dem Boden gestützt wird.

Wenden wir dieses Konzept auf die Übertragung der erheblichen Lasten der Auslegerfüße in den Untergrund an. Die relevante Struktur ist die Kranmatte. Ihre Aufgabe ist es, die beträchtliche Punktlast des Auslegerfußes auf der Erdoberfläche zu verteilen. (Wir gehen davon aus, dass die Matte ausreichend steif ist, sodass Biegung kein Problem darstellt. Wenn Sie sich eingehender mit der Abstützung von Kränen am Boden befassen möchten, sollten Sie sich ein Exemplar von David Duerrs „Mobile Crane Support Handbook“, 2. Auflage 2019, besorgen.)

Im Standardfall (Fall a in Abbildung 3) befindet sich die Baggermatte mittig unter dem Stützfuß. Wenn Sie einen Ingenieur bitten, den Bodendruck unter Ihrem Stützfuß zu berechnen, wird dieser angenommen. Der Druck unter der Baggermatte ergibt sich einfach aus der Gesamtlast geteilt durch die Fläche der Baggermatte (auch hier vernachlässigen wir die Biegung und gehen von einer 100%igen Wirksamkeit der Matte aus). Also GBP, w = P/A, wobei w = Bodendruck (psf), P die Stützfußlast (lbs.), A die Fläche der Baggermatte (ft2) ist.

Wenn Sie die Matte etwas außermittig platzieren, erhöht sich der maximale Bodendruck unter der Matte, wie in Abbildung 3b dargestellt. Beachten Sie, dass der durchschnittliche Bodendruck unter der Matte unverändert bleibt. Je nach Bedingungen kann dies akzeptabel sein (oder auch nicht).

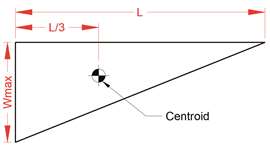ABBILDUNG 4: Das Dreieck.

Sobald der Ausleger über das mittlere Drittel der Matte hinausgeschoben wird (Abbildung 3c), ist die Belastung am anderen Ende der Matte gleich Null. Der Schwerpunkt des Dreiecks (dort befindet sich sein Schwerpunkt) beträgt nämlich ein Drittel der Schenkellänge (Abbildung 4).

Da die Gesamtlast weiterhin getragen werden muss und die Fläche eines Dreiecks ½ der Grundfläche x Höhe entspricht, ist der maximale Druck unter der Matte nun doppelt so hoch wie bei zentriertem Ausleger. Die gesamte Mattenoberfläche trägt die Last, der Druck auf den Boden ist jedoch ungleichmäßig. Dies ist wahrscheinlich nicht akzeptabel und sollte einer gründlichen Untersuchung unterzogen werden.

Überarbeiteter Standard

Im vergangenen Februar veröffentlichte die American Society of Mechanical Engineers (ASME) eine überarbeitete Fassung ihrer Norm P30-1 „Planung von Lasthandhabungsaktivitäten“. Die neue Ausgabe, ASME P30.1-2024, enthält einen neuen Anhang, den nicht verbindlichen Anhang D, der viele wichtige Themen im Zusammenhang mit der Abstützung von Kränen am Boden ausführlich behandelt.

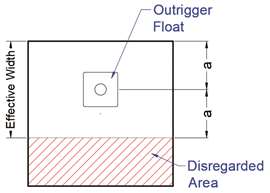ABBILDUNG 5: Effektive Mattengröße.

Passend zu unserer Diskussion hier bieten sie Hinweise zur exzentrischen Belastung von Stützplatten (Abschnitt D-8.4). Sie schlagen vor, falls es nicht möglich ist, den Stützteller auf der Matte zu zentrieren, eine effektive Fläche zu betrachten, bei der Breite und Länge um den Teller zentriert sind (siehe Abbildung 5). Die Fläche außerhalb dieser Symmetriefläche ist zu vernachlässigen. Die Skizze im Anhang veranschaulicht den allgemeinen Fall, bei dem der Teller in zwei Dimensionen verschoben wurde. In meiner obigen Diskussion gingen wir von einem Fall aus, bei dem der Teller in einer Dimension auf ein Drittel der Mattenbreite verschoben wurde. Somit würde die effektive Fläche in diesem Fall zwei Drittel der Mattenfläche betragen. Der durchschnittliche Bodendruck wäre dann 3/2 = 1,5-mal so hoch wie im Fall mit zentriertem Teller. Da die Verteilung jedoch ungleichmäßig ist, erhöht sich der Spitzendruck (wie oben gezeigt) um den Faktor zwei.

Sobald der Ausleger über das mittlere Drittel hinaus platziert wird (Abbildung 3d), trägt die gesamte Matte nicht mehr zur Lastaufnahme bei. Der Druck auf den Boden wird ungleichmäßig und steigt stark an. Vermeiden Sie dies. Bleiben Sie zentriert!

Geoffrey H Goldberg

Geoffrey H. Goldberg ist leitender Projektingenieur bei einem großen nationalen Kranbetreiber. Zuvor war er 20 Jahre lang als Brückenplaner in Pittsburgh, Pennsylvania, tätig.

Er ist der Autor von „Bridges: A Postcard History“ und mehreren Artikeln, die in American Cranes and Transport (ACT) erschienen sind.