Pourquoi rester centré est important : les leçons des cathédrales gothiques à la stabilité des stabilisateurs de grues modernes

FIGURE 2 : Pinacles de la cathédrale de Reims, achevés vers 1275.

Au Moyen Âge, les bâtisseurs de cathédrales utilisaient les structures qu'ils construisaient comme des maquettes grandeur nature, dans un processus organique où la réponse de la structure aux charges appliquées servait de signal aux constructeurs pour leur signaler la nécessité d'ajuster la conception. « Quel est le rapport avec l'utilisation de grues ? » vous demandez-vous sans doute. Soyez indulgents avec moi.

FIGURE 1 : Lignes de poussée dans une cathédrale gothique.

La caractéristique la plus identifiable des cathédrales gothiques est sans doute l'arc brisé (figure 1). Ces arcs fonctionnent en résistant aux forces de gravité grâce à des forces horizontales appelées poussées. La fonction de la structure est (comme le stabilisateur d'une grue) de placer ces charges dans le sol en toute sécurité. La combinaison de ces poussées avec le poids des blocs de pierre crée une ligne de poussées lorsque la charge suit son trajet vers le sol.

Lignes de poussée

Les constructeurs remarquèrent qu'à mesure que les structures prenaient de l'ampleur, des fissures apparaissaient dans les murs soutenant les arches. La conception des cathédrales était régie par le tracé de ces lignes de poussée. Idéalement, ces lignes devaient pointer directement vers le sol. Cependant, les poussées horizontales entravaient ce mouvement. De grands murs de pierre, appelés contreforts, furent construits pour résister à ces poussées. Et à mesure que les bâtiments s'agrandissaient, des arcs-boutants horizontaux furent ajoutés pour soutenir les murs supérieurs.

Ils ont découvert que si les lignes de poussée dépassaient largement le centre de la masse rocheuse, ces fissures apparaissaient. Leur solution consistait à les orienter verticalement en ajoutant des poids, appelés pinacles, au sommet des contreforts. C'est pourquoi ils ont ajouté ces magnifiques statues au sommet des structures (figure 2).

Au milieu du XIXe siècle, les ingénieurs ont commencé à quantifier le comportement des structures de maçonnerie.1 Au début des années 1900, le concept du « tiers médian » était largement utilisé dans la conception des structures de maçonnerie.

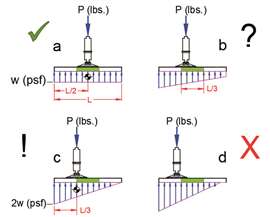FIGURE 3 : Stabilisateur soutenu par un tapis de grue sur le sol.

Appliquons ce concept au problème de la transmission des charges importantes des stabilisateurs au sol. La structure étudiée est le tapis de grue. Son rôle est de répartir la charge ponctuelle importante des stabilisateurs à la surface du sol. (Nous supposerons que le tapis est suffisamment rigide, la flexion ne pose donc pas de problème. Pour approfondir le sujet du stabilisateur des grues au sol, nous vous recommandons de vous procurer un exemplaire du Manuel de stabilisateurs de grues mobiles de David Duerr, deuxième édition, 2019).

Le cas « standard » (cas a de la figure 3) est celui où le tapis de la grue est centré sous le flotteur du stabilisateur. Lorsqu'un ingénieur calcule la pression d'appui au sol sous le stabilisateur, il s'agit de la condition supposée. La pression sous le tapis de la grue correspond simplement à la charge totale divisée par la surface du tapis (là encore, nous ignorons la flexion et supposons que le tapis est efficace à 100 %). Donc GBP, w = P/A où w = pression d'appui au sol (lb/pi²), P est la charge du stabilisateur (lb), A est la surface du tapis de la grue (pi²).

Si vous décalez légèrement le tapis, la pression maximale au sol augmentera sous le tapis, comme illustré à la figure 3b. Notez que la pression moyenne au sol sous le tapis reste la même. Selon les conditions, cela peut être acceptable (ou non).

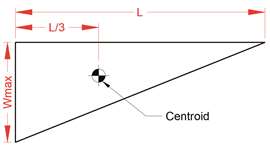FIGURE 4 : Le Triangle.

Une fois le stabilisateur poussé au-dessus du tiers médian du tapis (figure 3c), la charge à l'extrémité du tapis est nulle. En effet, le centre de gravité du triangle (où se situe son centre de gravité) représente un tiers de la longueur de la jambe (figure 4).

Étant donné que la charge totale doit encore être supportée, et sachant que l'aire d'un triangle est égale à la moitié de la base x la hauteur, la pression maximale sous le tapis est désormais deux fois supérieure à celle du cas a avec le stabilisateur centré. Toute la surface du tapis est sollicitée pour résister à la charge, mais la pression au sol est inégale. Cette situation est peu susceptible d'être acceptable, et une évaluation sérieuse doit être effectuée.

Norme révisée

En février dernier, l'American Society of Mechanical Engineers (ASME) a publié une révision de sa norme P30-1, Planification des activités de manutention de charges. La nouvelle édition, ASME P30.1-2024, comprend une nouvelle annexe, l'annexe D non obligatoire, qui traite de nombreux sujets importants liés au support des grues au sol.

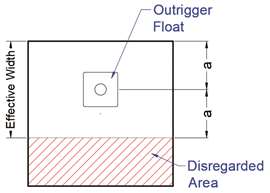FIGURE 5 : Taille effective du tapis.

À propos de notre discussion, ils fournissent des conseils pour la charge excentrique des patins de stabilisateur (section D-8.4). Ils suggèrent que, s'il n'est pas possible de centrer le flotteur de stabilisateur sur le tapis, il faut considérer une surface effective telle que les dimensions de largeur et de longueur soient centrées autour du flotteur (voir figure 5). La surface extérieure à la zone de symétrie est à négliger. Le schéma présenté en annexe illustre le cas général où le flotteur a été décalé dans deux dimensions. Dans ma discussion ci-dessus, nous avons supposé un cas où le flotteur a glissé dans une seule dimension sur un tiers de la largeur du tapis. Ainsi, la surface effective dans ce cas serait égale aux deux tiers de la surface du tapis. La pression au sol moyenne serait alors de 3/2 = 1,5 fois la pression du cas avec le flotteur centré. Mais comme la distribution est inégale, la pression maximale (comme je l'ai montré ci-dessus) est multipliée par deux.

En allant plus loin, une fois le stabilisateur placé au-delà du tiers médian (figure 3d), le tapis ne résiste plus à la charge et la pression au sol est inégale et augmente considérablement. Évitez cela. Restez centré !

Geoffrey H. Goldberg

Geoffrey H. Goldberg est ingénieur de projet senior chez un important grutier national. Auparavant, il a passé 20 ans à concevoir des ponts à Pittsburgh, en Pennsylvanie, la « ville des ponts ».

Il est l'auteur de Bridges: A Postcard History et de plusieurs articles parus dans American Cranes and Transport (ACT).