Por que permanecer centrado é importante: lições das catedrais góticas à estabilidade dos estabilizadores de guindastes modernos

FIGURA 2: Pináculos da Catedral de Reims, concluída por volta de 1275.

Os construtores de catedrais na Idade Média usavam as estruturas que construíam como modelos em escala real, em um processo orgânico em que a resposta da estrutura às cargas aplicadas servia como um sinal para os construtores de que ajustes no projeto eram necessários. "Que diabos isso tem a ver com a operação de guindastes?", você provavelmente está se perguntando. Tenha paciência comigo.

FIGURA 1: Linhas de empuxo em uma catedral gótica.

A característica mais identificável das catedrais góticas é, sem dúvida, o arco pontiagudo (Figura 1). Esses arcos funcionam resistindo às forças da gravidade com forças horizontais chamadas de empuxos. A função da estrutura é (como a de um guindaste) cravar essas cargas no solo com segurança. A combinação desses empuxos com os pesos dos blocos de pedra resulta em uma linha de empuxos à medida que a carga segue seu caminho até o solo.

Linhas de impulso

Os construtores notaram que, à medida que as estruturas aumentavam de tamanho, rachaduras se formavam nas paredes que sustentavam os arcos. O projeto das catedrais era regido pelos caminhos que essas linhas de empuxo percorriam. Idealmente, as linhas deveriam apontar diretamente para o chão. No entanto, os empuxos horizontais dificultavam isso. Grandes muros de pedra, chamados contrafortes, foram construídos para resistir a esses empuxos. E, à medida que os edifícios aumentavam de tamanho, braços horizontais, chamados arcobotantes, foram adicionados para sustentar as paredes superiores.

Eles descobriram que, se as linhas de empuxo viajassem muito além do centro da massa de pedra, essas rachaduras apareceriam. A solução foi girar as linhas de empuxo para a vertical adicionando pesos, chamados pináculos, ao topo dos contrafortes. Essa é a razão pela qual eles adicionaram aquelas estátuas maravilhosas ao topo das estruturas (Figura 2).

Em meados do século XIX, os engenheiros começaram a quantificar o comportamento das estruturas de alvenaria.1 No início dos anos 1900, o conceito de “terço médio” era bem utilizado no projeto de estruturas de alvenaria.

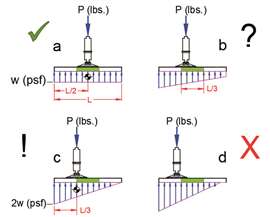FIGURA 3: Estabilizador apoiado sobre esteira de guindaste no solo.

Vamos aplicar este conceito ao problema de transferir as cargas significativas dos flutuadores dos estabilizadores para o solo de suporte. A estrutura de interesse é a esteira do guindaste. Sua finalidade é distribuir a carga pontual considerável do flutuador dos estabilizadores ao longo da superfície do solo. (Assumiremos que a esteira é suficientemente rígida, portanto, a flexão não é um problema. Se você quiser explorar o assunto do suporte de guindastes no solo com mais profundidade, você deve adquirir um exemplar do Manual de Suporte para Guindastes Móveis de David Duerr, Segunda Edição, 2019).

O caso "padrão" (Caso a na Figura 3) é onde a manta do guindaste está centralizada abaixo da flutuação do estabilizador. Quando você pede a um engenheiro para calcular a pressão de apoio no solo abaixo do seu estabilizador, esta é a condição assumida. A pressão sob a manta do guindaste é simplesmente a carga total dividida pela área da manta do guindaste (novamente, aqui estamos desconsiderando a flexão e assumindo que a manta é 100% efetiva). Portanto, GBP, w = P/A onde w = pressão de apoio no solo (psf), P é a carga do estabilizador (lbs.), A é a área da manta do guindaste (ft²).

Se você posicionar o tapete um pouco descentralizado, a pressão máxima de apoio no solo aumentará abaixo do tapete, como mostrado na Figura 3b. Observe que a pressão média de apoio no solo abaixo do tapete permanece a mesma. Dependendo das condições, isso pode (ou não) ser aceitável.

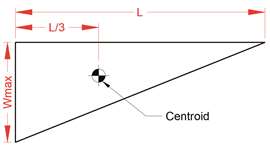FIGURA 4: O Triângulo.

Ao empurrar o estabilizador para fora, acima do terço central do tapete (Figura 3c), a carga na extremidade oposta do tapete é zero. Isso ocorre porque o centroide do triângulo (onde se localiza o centro de gravidade) é um terço do comprimento da perna (Figura 4).

Como a carga total ainda precisa ser resistida, e lembrando que a área de um triângulo é ½ da base x altura, a pressão máxima sob o tapete é agora o dobro do que era no caso de um estabilizador centralizado. Toda a superfície do tapete está envolvida na resistência à carga, mas a pressão sobre o solo é desigual. É improvável que isso seja aceitável, e uma avaliação criteriosa deve ser realizada.

Padrão revisado

Em fevereiro passado, a Sociedade Americana de Engenheiros Mecânicos (ASME) publicou uma revisão de sua norma P30-1, Planejamento para Atividades de Movimentação de Carga. A nova edição, ASME P30.1-2024, inclui um novo Apêndice, o Apêndice D Não Obrigatório, que aborda com propriedade muitos tópicos importantes relacionados ao suporte de guindastes em solo.

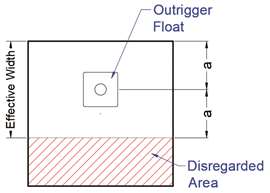FIGURA 5: Tamanho efetivo do tapete.

A propósito da nossa discussão aqui, eles fornecem orientação para carga excêntrica de sapatas de estabilizadores (seção D-8.4). Eles sugerem que, se não for possível centralizar o flutuador do estabilizador sobre o tapete, considere uma área efetiva tal que as dimensões de largura e comprimento estejam centralizadas em torno do flutuador (ver Figura 5). A área fora da área de simetria deve ser desconsiderada. No esboço que eles apresentam no Apêndice, o caso geral em que o flutuador foi deslocado em duas dimensões é ilustrado. Na minha discussão acima, presumimos um caso em que o flutuador foi deslizado em uma única dimensão para um terço da largura do tapete. Assim, a área efetiva para este caso seria dois terços da área do tapete. A pressão média sobre o solo seria então 3/2 = 1,5 vezes a pressão do caso com o flutuador centralizado. Mas, como a distribuição é desigual, a pressão de pico (como mostrei acima) é multiplicada por dois.

Indo mais além, uma vez que o estabilizador é posicionado além do terço médio (Figura 3d), todo o tapete não está mais envolvido na resistência à carga e a pressão sobre o solo é desigual e aumenta consideravelmente. Não faça isso. Mantenha-se centrado!

Geoffrey H Goldberg

Geoffrey H Goldberg é engenheiro sênior de projetos em uma grande operadora de guindastes dos Estados Unidos. Anteriormente, passou 20 anos projetando pontes na "Cidade das Pontes" — Pittsburgh, Pensilvânia.

Ele é autor de Bridges: A Postcard History e de vários artigos que apareceram na American Cranes and Transport (ACT).